(Click to Enlarge)

This Packing Puzzle is made from laser cut wood and it's comprised of nine identical triangles. It is relatively small, with the frame measuring just over 10cm (about 4") and each triangle measuring exactly 2.6cm (1"). The packing area is an exact square with 6cm in length. Inside the frame there are eight triangles and there's a slot in the frame's border to store the extra triangle. The goal, as it would be expected, is to try packing the ninth triangle inside the tray as well. Note that the pieces won't fill the entire tray area. Pretty simple, but it can be rather tricky.

The design is very well made, with the name of the puzzle nicely engraved onto the frame. The contrast between the frame's light color and the dark tone of the triangles is also perfectly achieved, as it brings more focus to the main feature of the puzzle, the triangles.

Solving the Dreiecksbeziehung puzzle was a lot harder than I would expect, mainly because it's rated by PuzzleMaster as a 6/10, which is considered an easy puzzle. Despite the apparent easiness and after I've spent close to two hours between three attempts, I wouldn't consider this an easy puzzle, at all. Probably more like a 7 or 8/10.

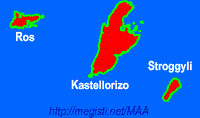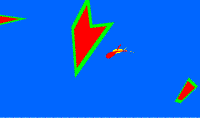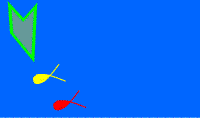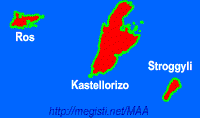
What I found harder is that no matter how I would try to rearrange the pieces, it would always leave just a tiny portion of the triangle out of the frame. My understanding was that the final solution had to be extremely tight, and I also believed that it probably wouldn't be a symmetrical arrangement as I first thought. Both my assumptions proved to be correct in the end, when I finally packed that damned ninth triangle.

Since, as I thought, the fit between the pieces was so tight (no wobble), I had to check the solution to see if I did it right. Apparently I did, but the solution was a bit different from mine, so I tried to pack the pieces that way as well. As I suspected, PuzzleMaster's solution was just as tight as mine. For you to have an idea of the tightness I'm talking about, you need to apply a bit of down force to the last piece in order to fit in the tray... And it's not easy to remove the pieces once they're all packed. Be careful, as you might break a piece in the process. You can see both solutions, PuzzleMaster's and mine.

(Click to Enlarge) - Not Solved

Closing Comments:

I really liked the challenge of the Dreiecksbeziehung and of course, its elegant design. While it was harder than I was expecting, I liked the fact that I had to spend more time with a great puzzle. It wouldn't be so fun, had I just solved it in five or ten minutes now would it? When you spend twenty dollars or more on a puzzle, you expect it to be worth it, not be done with it in a heartbeat.

Links:


Triangles in Squares - Eric Friedman's page about packing triangles (1 to 27) into the smallest known square