Puzzle Impossible
Share
(Click to Enlarge)
The Cast Puzzle Series may be the hallmark product produced by Hanayama, but they have many other different challenges and they're very interesting as well.
The Puzzle Impossible is a good example of the Hanayama's quality and originality. It was designed by Ukrainian Serhiy Grabarchuk Jr. and it's a Slide Puzzle with a twist. This ingenious design depicts the numbers from 1 to 9, in a 3x3 grid, in the digital form of seven-segment display characters. The "twist" is that the segments from each number aren't all printed on the transparent tiles - some of them are marked on the tray. This way, as you slide each tile inside the frame, the number appears to be scrambled as if your digital wrist watch/alarm clock was out of whack. This cool effect is what makes the design so appealing.
There are three main challenges that you can attempt to solve (just by sliding the tiles). The packaging of the puzzle is entirely in Japanese, however, it's easy to recognize by the pictures what needs to be accomplished. The first challenge is common to every slide puzzle - just scramble the tiles and then return them to their original pattern. This is relatively easy for anyone that has solved the classic 15 Puzzle. The next two challenges are exactly what gives this puzzle its "Impossible" connotation.
(Click to Enlarge)
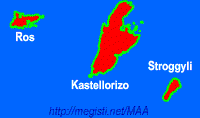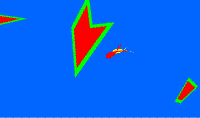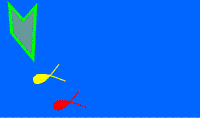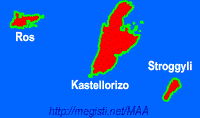
The second challenge, or first of these two impossible tasks, requires you to swap the last two tiles by making a sequence of 1, 2, 3, 4, 5, 6, 7, 9, 8 and solve it into the correct arrangement. Now, if you're familiar with the slide puzzle concept and history, you know that the presented challenge will create a parity error, because it requires a transformation of an even combination to an odd one. But there's a way to overcome that by taking advantage of the puzzle's concept. Spoiler ahead: If you look closely at the photo of the tiles outside the tray (above this paragraph), you can see that the segments that form the number 4 are exactly the same as the ones on the number 9. By making the "4" and "9" tiles swapping places, it becomes possible to solve the puzzle. There is a minimum of 18 moves to solve this.
(Click to Enlarge) - Challenge 2 - Left: Initial State; Right: Goal
The final challenge is another impossibility: from the solved state, you are now required to make an arrangement of the tiles, also just by sliding, so that it shows the sequence 1, 2, 3, 4, 5, 6, 7, 8, 3. Again, how is it possible to have two of the same numbers appear on the same frame? - There are two solutions for this, one that uses a minimum of 24 moves and another with only 20 moves. Spoiler ahead: By looking again at the photo of the tiles outside the tray, there are exactly two tiles that can form the number 3 on the frame. One is being used by the "3" in the first row, and the other is being used to form the "7". The first think that comes to mind is, "how to show in the same frame a 3, a 7 and another 3?" - The answer lies in the way you can form a 7. The first is just with three segments and the other, the solution, is with four (see the difference in the photo, below right). So, the first solution requires a swap of the "3", "7" and "9" tiles to the positions of the "9", "3" and "7", respectively. The second solution, more efficient, requires a swap of the tiles "4", "7", "9" to the positions "7", "9", "4", respectively. Intuitively, it would be more practical to just swap the number 7 with the 9, but it would result in another parity error.
(Click to Enlarge) - Challenge 3 - Left: Initial State; Right: Goal
I have seen this puzzle for the first time, a while ago at Rob's Puzzle Page, but whenever I tried to buy one, I couldn't find it anywhere. That was until a couple of months ago, when I found one for sale at eBay. I had to get it before it was too late again. At the time I bought this one, the seller had another copy, but now, unfortunately, it seems to have gone. I checked Hanayama's website, but couldn't find it there either. I believe they're being sold at Amazon Japan, but I'm not sure they send overseas. It was apparently a limited production run and now it's harder to find.
Closing Comments:
It seems that almost anything was attempted with the sliding puzzle concept before, but Serhiy Grabarchuk Jr. proved that it's still very possible to come up with an original and amazing design... And associated with Hanayama's quality, you can't go wrong with the Puzzle Impossible. Definitely recommended for the Sliding Tile enthusiasts... If you find one.




































2 comments:
In Grabarchuk's app, there is a version of the 3x3 grid with the 8 and 7 transposed. What seems to make it possible is that pieces are not square tiles, but the shapes of the numbers. For example, a configuration that generates a lot of extra space is to nest the 7 along the back of the 1.
Despite that "insight," I still can't get enough space to effect the transposition.
Have you solved it? Any hint that you can offer that doesn't completely give away the solution?
FWIW, the most dense nesting I have been able to find generates extra free space of 2/3 the area of the "square" pieces (2,5,6 or 8).
Hi Joshua,
I haven't played that puzzle app, so can't help you there. You can always try to send an e-mail to Grabarchuk and ask for a hint.
Post a Comment